Distances on Globe and Flat Earth
Autor: Walter Bislin
Original: walter.bislins.ch/bloge/index.asp?page=Distances+on+Globe+and+Flat+Earth
I derive the formulas to compute the distance between two points for both models. The computations can be carried out using a calculation form. An example is then used to decide which model corresponds to reality.
Calculation Form
You can enter Latitude/Longitude in degrees with decimal point (e.g. 54.5°) or degrees, minutes and seconds (e.g. 54° 30min). Latitudes on the Southern Hemisphere and Longitudes westerly of the 0-Meridian must be entered as negative values. See Input Format for Latitude and Longitude for some input examples.
Perth-Sydney Johannesburg-Perth London-Moskau
The distance between 2 points P1 and P2 is computed on a Globe width radius R and on Flat Earth with distance from north pole to equator EQ. If you want to use other planet sizes, enter your values into the corresponding fields, else leave them as is. You can reset the fields to their default values by clicking into the fields and pressing the ESC key.
You can choose the units you want the distances to be calculated as km, nautical miles (nmi) or statute miles (mi).
Input Format for Latitude and Longitude
The 3 fields for Latitude and Longitude accept all common input formats. You can enter the latitude or longitude using only the degrees field when entering any common format or enter it in degrees, minutes and seconds in the corresponding fields. You can set N,S,E or W before or after the number in the dregrees field or use negative numers for S and W.
- All in degrees: 51.507351° | 120 58 57W | 120°58’57″W | W69 01 29.74 | 41 25N | N41 25.117 | 32 S
- Enter the value into the Degree-Field and leave the Minute and Second field 0.
- Degrees and Minutes: 51° 30.44106 min
- Enter the whole degrees into the Degree-Field and the minutes into the Minute field and leave the Second field 0.
- Degrees, Minutes and Seconds: 51° 30 min 26.4636 sec
- Enter each part into the corresponding field.
If you have a negative Latitude or Longitude with the zero degrees then enter 0 for degrees and a negative minute: 0° −7 min 39.929 sec. If Degree and Minute are zero, enter the negative sign into the Second field: 0° 0 min −12.34 sec.
Use the button →DMS to convert from Degree-Format to Degree-Minute-Second-Format. Use the button →Deg to convert from Degree-Minute-Second-Format to Degree-Format. This is useful to copy the position to google earth as one value.
Which Model fits Reality?
Flat Earth and Globe Earth are two models for the earth that are very different in geometry. Lets assume we don’t know yet the right shape. On both models exists a way to define the shortest distance between two points. A point is defined on both models by a degree of latitude and longitude. The point with the same latitude and longitude correspond on both models to the same location, e.g. a certain city. We can derive for both models a formula to compute the distances. So we can make a corresponding prediction for both models. In order to decide which model is the correct one, we can calculate the shortest distance between the same two points for both models and check which prediction matches reality. If we find two points that give very different predictions for the two models, it is easy to figure out the right model.
On the globe earth the shortest distance is the so-called Great-circle distance, on the flat earth this is a straight line.
The real distance has to be gained by experiment, that means measuring the real world, not by distance indications on maps, since from this distance the correct model should be deduced. We can get the real distance between two locations by measuring the flight time of a direct flight between two locations and multiplying it by the average flight speed. Time and speed of a commercial airplane over a sufficient great distance give a good estimate for the real distance.
In order to obtain a clear result, we use distances which are as different as possible in both models for the same two locations. These are mainly distances in the southern hemisphere.
I choose the distance between Perth and Sydney Australia. Because they lie on the same continent this distance could also be obtained by driving with a car between this cities. The following dataset is used for both models:
| Dataset | |
|---|---|
| Perth (PER) | Latitide = -31.950527, Longitude = 115.860457 |
| Sydney (SYD) | Latitude = -33.868820, Longitude = 151.209296 |
| Flight-Time SYD/PER TSP | 5 h 05 min = 5.08 h, from expedia.com for Qantas A330-200 |
| Flight-Time PER/SYD TPS | 4 h 10 min = 4.17 h, from expedia.com for Qantas A330-200 |
| Ground Speed SYD/PER VSP | 427 kts = 791 km/h, from flightradar24.com for A330-200 |
| Ground Speed PER/SYD VPS | 535 kts = 991 km/h, from flightradar24.com for A330-200 |
| Taxi-Time TTaxi | 20 min = 0.33 h, from www.rita.dot.gov, United States Department of Transportation |
| Hold-Time THold | 10 min = 0.17 h, reserve time for holding patterns and vectors |
| Taxi+Hold TTH | 30 min = 0.5 h |
| Climb/Descent-Time TCD | 43% · 1.5 h = 0.645 h, from www.cfidarren.com, Statistical Summary of Commercial Jet Airplane Accidents |
See Umrechnen von Fluggeschwindigkeiten how speeds are converted.
The Taxi and Hold times must be subtracted from the Flight-Times to get the time relevant for the distance traveled. During the Climb and Descent time the speed is increasing/decreasing. So I take the mean speed for this period. That is half of the cruise speed. The climb/descent time is for all flights the same and I found a value of 43% · 1.5 h = 0.645 h here which matches my experience with flight simulator times.
The formula to compute the distance traveled is then:
| (1) |
|
|||||||||||||||
| where‘ |
|
Lets compute the distance from Sydney to Perth:
| (2) |
|
Now lets compute the distance from Perth to Sydney:
| (3) |
|
The difference is about 1.5%. The real distance is some km shorter because the airports are not aligned with the flight track so the airplane diverges after start and before landing some km from the direct route.
Result
The shortest distances computed between Perth and Sydney for the two models, according to the Calculation Form, are:
| Globe Earth Model | Flat Earth Model | Flight Distance SYD/PER | Flight Distance PER/SYD |
|---|---|---|---|
| 3291 km | 8301 km | 3368 km (2) | 3317 km (3) |
The Flat Earth Model is wrong by a factor of 2.5!
Check it Yourself
Google Maps gives a Distance from Perph to Sydney along a road of 3934 km. You can drive this route with your car and check the distance with your car’s odometer. The distance is much shorter than what the Flat Earth model predicts.
To check whether the latitude and longitudes are correct on this page, you can buy a cheap Sextant e.g. on Amazon and measure the coordinates yourself using Celestial navigation technique.
Submarine Cables
Some flat earther claim submarine cables somehow prove the earth is flat. But if you look closer, they prove the earth can not be flat at all, on the contrary:
On the website Submarine Cable Map you can see all cables and get Infos about it. For example the cable between Sydney and Perth is 4850 km long:
| RFS | Q1 2019 |
| Cable Length | 4850 km |
| Owners | Superloop, SingTel, Google, Indosat Ooredoo, Australia’s Academic and Research Network (AARNET) |
| URL | http://www.subpartners.net/indigo |
The cable follows not the shortest line between this cities (3290 km) because it has to follow the shore line. So its length is 4850 km. The shortest line on the flat earth map is 8300 km between Sydney and Perth. So even the shortest connection on the flat earth is 1.7 times longer than the cable that follows the shore line.
Used Formulas for Globe Earth
Note: To prove that the following formulas are used in the calculations, you can insepct the Source Code of this Page. 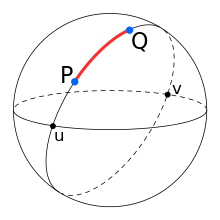 On a Globe the shortest distance between 2 points is a great circle.
On a Globe the shortest distance between 2 points is a great circle.
The points are given in polar coordinates latitude and longitude :
| (4) | |||||||
| (5) | |||||||
| where‘ |
|
Converting into cartesian vector format using the center of the sphere as (0,0,0):
| (6) | ||||||||||
| (7) | ||||||||||
| width | ||||||||||
| where‘ |
|
The unit vectors to the 2 points are:
| (8) | ||||||||||
| (9) | ||||||||||
| where‘ |
|
The cosine of the angle between the vectors is:
| (10) |
And the great circle distance between the Points is:
| (11) | |||||||||||||
| where‘ |
|
Expressed in a single equation we get:
| (12) | |||||||||||||
| where‘ |
|
If we set and we can (12) further simplify to:
| (13) |
|
Used Formulas for Flat Earth
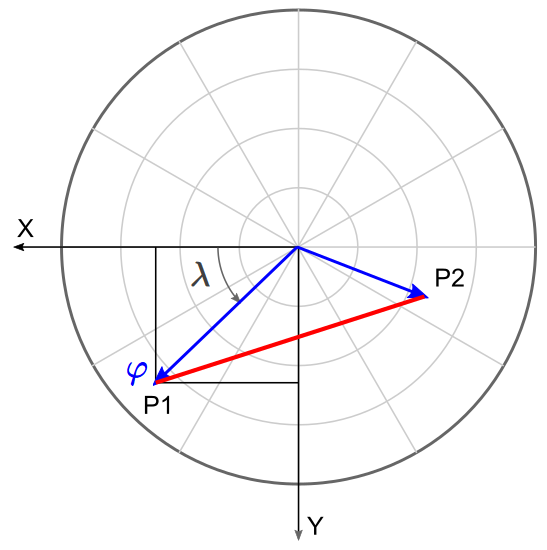 I first convert the points polar coordinates to cartesian coordinates. Then the points are 2 vectors in cartesian coordinates. Subtracting one vector from the other and computing the lengt of the resulting vector gives the distance between the 2 points on a flat earth, which is a straight line.
I first convert the points polar coordinates to cartesian coordinates. Then the points are 2 vectors in cartesian coordinates. Subtracting one vector from the other and computing the lengt of the resulting vector gives the distance between the 2 points on a flat earth, which is a straight line.
The length ri of the vector i from the north pole to a point Pi(φ,λ) is:
| (14) | ||||||||||
| where‘ |
|
Explanation
If the latitude is 0, then r sould be the distance of the equator from the north pole E. If latitude is positive, then r should decrease by the amount . So if latitude is 90°, the amount of decrease is Δ r = (90° / 90°) · E = E, i.e. at the north pole r = E − Δ r = 0. Accordingly if the latitude is negative, the distance from the equator should increase. This gives the equation for the distance of a latitude from the north pole:
| (15) |
where the latitude is given in degrees. After factoring out E and if we have the latitude given in radian, we get the formula (14).
Having the length of the vector together with its longitude, the cartesian coordinates of Pi can be computed:
| (16) | |||||||
| (17) | |||||||
| where‘ |
|
The distance between the points P1 and P2 is:
| (18) |
Expressed in a single equation we get:
| (19) | ||||||||||
| where‘ |
|
If we set and we can (19) further simplify to:
| (20) |
|
|
| with |
Note: this is nothing else than the Law of cosines for a triangle with sides r1, r2 and angle λ for the unknown side L.











TikTok: tiktok.com/@olegmks
ВКонтакте: vk.com/olegmks
YouTube: youtube.com/c/OlegMKS
Яндекс.Дзен: zen.yandex.ru/olegmks
RuTube: rutube.ru/channel/23320330/